1、傅里叶变换性质有线性位移微分积分1线性性质函数线性组合的傅里叶变换=各函数傅里叶变换的线性组合 2位移性质shift信号偏移傅里叶变换,时移性如ftt0表示时间函数ft沿t轴向右平移t0傅里叶变换,其傅里叶变换=ft的傅里叶变换乘以因子expiwt0傅里叶变换,类似ft+t0的傅里叶。
2、1由三倍角公式sin#179t=3sint4sin#179t傅里叶变换,得sin#179t=3sintsin3t42则sinat的傅里叶变换为jπδw+aδwa3所以ft的傅里叶变换为Fw=jπ3δw+13δw1δw+3δw344化简得Fw=πi4。
3、傅里叶变换的四种基本形式包括傅里叶级数FS连续傅立叶变换CTFT离散时间傅立叶变换DTFT和离散傅立叶变换DFT1 傅里叶级数FS定义傅里叶级数适用于周期连续时间信号傅里叶变换,它将一个周期信号分解为一系列正弦和余弦函数的和特点在频域上,傅里叶级数表现为离散非周期的频谱。
4、快速傅里叶变换FFT 通过利用DFT的周期性和对称性,将计算分解为多个短序列DFT的迭代例如,按时间抽取的FFT算法将长序列按奇偶分组,递归分解为2点DFT,最终将复杂度降至 ON log N 这一突破使得实时信号处理成为可能,广泛应用于通信图像压缩等领域3 FFT的分类与实现FFT算法主要分。
5、傅里叶变换是一种将信号从时间域或空间域转换到频率域的数学工具,它可以表示信号中的各个频率分量逆傅里叶变换则是将频率域的信号转换回时间域的操作一傅里叶变换与逆傅里叶变换的定义 傅里叶变换定义对于一个可积的函数 $ft$,其傅里叶变换 $Fomega$ 定义为Fomega。
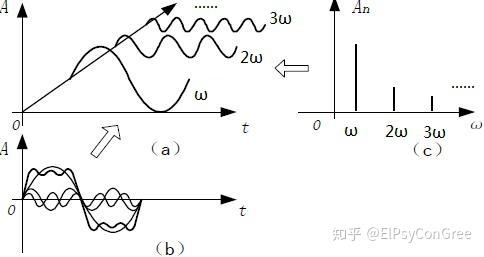
6、傅里叶变换的本质,就是用各种频率不同的周期函数频域线性表示原始函数时域,必然具有线性性这与积分的线性性是一致的 线性性质可用图1来概括先变换再求和,与先求和再变换,结果是一致的 2位移性 设mathscr Fft=Fomegamathscr Fft=Fomega,t_0,omega_0t_0,omega_。
7、1 线性性傅里叶变换是线性的,即对于任意两个信号ft和gt,以及任意实数a和b,有Faft+bgt=aFft+bFgt2 对称性傅里叶变换具有对称性,即ft的傅里叶变换Fω与Fω对称3 移位性ft在时域上的移位,相当于在频域上进行相位旋转,即Ff。
8、1的傅里叶变换是指将一个常数函数1在傅里叶变换中的表示傅里叶变换是一种数学变换,用于将一个函数表示为一组正弦和余弦函数的线性组合对于常数函数1,它的傅里叶变换表示为一个脉冲函数,即在频域上的表示为一个常数幅度的正弦函数这意味着常数函数1在频域上没有频率成分,只有一个幅度成分。
9、傅里叶变换是一种数学工具,用于将一个函数或信号从时域时间域转换到频域在数学上,傅里叶变换有多种形式,其中最常用的两种是连续傅里叶变换和离散傅里叶变换连续傅里叶变换Continuous Fourier Transform请点击输入图片描述 离散傅里叶变换Discrete Fourier Transform,DFT请点击。
10、指数函数单边ft=eatut Fw=1,实际上是一个低通滤波器a+jw常用函数的傅里叶变换公式表如下1门函数Fw=2w w sin=Sa w2指数函数单边ft=eatut Fw=1,实际上是一个低通滤波器a+jw3单位冲激函数Fw=1,频带无限宽,是一个均匀谱4。

11、Fjw=πδww0πδw+w0j求fx=sinw0t的傅里叶变换w0为了与w区分根据欧拉公式得sinw0t=e^jw0te^jw0t2j因为直流信号1的傅里叶变换为2πδw而e^jw0t是直流信号傅里叶变换的频移所以e^jw0t的傅里叶变换为2πδww0,同理e^jw0。
12、傅里叶变换并没有一个固定的“十大公式”列表,但以下是根据傅里叶变换的核心概念和常见形式总结出的几个关键公式和类别非周期性连续信号傅里叶变换公式$F = int_infty^infty fe^jomega tdt$描述将非周期性连续信号$f$转换为频域表示$F$周期性连续信号傅里叶级数公式$f。
13、傅里叶变换是一种在数学物理和工程中广泛使用的分析工具,它可以将一个函数或信号从时域时间转换到频域频率傅里叶变换之间相互的关系主要体现在以下几个方面时域与频域的对应关系傅里叶变换的核心思想是将一个复杂的信号分解为一系列简单的正弦波和余弦波的叠加这些正弦波和余弦波的频率和振幅分别对应着信号的频域特性。
14、这是“补零”的一个用处第二种是采用以任意数为基数的FFT算法频谱就是以2*fs为周期的,分辨率依然是1若是先把Fw里的w变量换成 t, 得到Ft再对Ft进行傅里叶变换这时,我们可以将图片第二行的等式两边的 t 换成w, 原来的w换成 t 得到结果为2πfw。
15、傅里叶变换的四种意义如下数学变换工具傅里叶变换是一种线性算子,在线性代数和函数分析中扮演着重要角色若赋予适当的范数,它还是酉算子,这意味着它在变换过程中保持了向量的长度不变,具有保范性逆变换的简易性傅里叶变换的逆变换容易求出,且形式与正变换非常相似这种可逆性使得傅里叶。
16、三角波的傅里叶变换公式是ft是t的周期函数,如果t满足狄里赫莱条件在一个以2T为周期内fX连续或只有有限个第一类间断点,附fx单调或可划分成有限个单调区间,则Fx以2T为周期的傅里叶级数收敛,和函数Sx也是以2T为周期的周期函数傅立叶变换,表示能将满足一定条件的某个。