1、主成分分析PCA是一种通过正交变换将一组变量转换成另一组变量pca分析的统计方法pca分析,主要用于数据降维转换后pca分析的这组变量即为主成分pca分析,它们能够反映原始数据的主要特征,同时减少数据的复杂性一PCA的基本原理 主成分的定义主成分是由原始变量通过线性组合得到的新变量这些新变量主成分在总方差中所占的比例依次递减,即第一主成。
2、PCA基于线性模型开展,适用于物种少环境因素和物种丰度波动变化小的情况PCA分析能够直观地展示样本间的分布和差异,但不适用于物种丰度变化范围大或环境梯度变化大的样本PCoA常用于微生物β多样性分析中,能够反映样本间的相似距离PCoA分析的结果受相似性距离计算方式的影响,因此不同相似性距离计。
3、PCA,即主成分分析Principal Component Analysis,是一种统计方法,用于通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,这些新的变量被称为主成分PCA图则是将PCA分析的结果以图形化的方式展示出来,便于直观地理解数据的主要特征和结构二PCA图的作用 降维PCA图通过提取数据。
4、主成分分析PCA是一种用于数据降维的方法首先,pca分析了解降维的目的是减少数据维度,同时尽量保持数据的原始信息举个例子,我们可以利用房价数据来说明这个过程假设我们有一个数据集,包含了房价和面积两个特征为了进行降维,我们需要先对数据进行中心化处理,即将每个特征的数值减去各自的均值这样做是。
5、PCA主成分分析是一种利用线性变换进行数据降维和去噪的方法,其核心在于保留数据的主要信息 主要信息通常指能够最大程度区分数据类别的信息,在数学上通过数据的方差来衡量离散程度以下是PCA的关键步骤和原理数据标准化首先对原始数据 D n 维 k 组进行中心化处理,即减去。
6、主成分分析PCA是一种用于数据降维和特征提取的无监督学习方法以下是对PCA的详细解释一PCA的核心概念 PCA的目标是找到一个新的坐标系统来表示数据,这个新坐标系统的基向量坐标轴是从数据本身中提取出来的这些新的坐标轴或称为主成分按照解释数据中变化的能力来排序第一主成分代表。
7、PCA主成分分析PCA是一种数据降维的方法,它从高维数据中提取数据的特征向量成分,转换为低维数据,并用二维或三维的图来展示这些特征从特征向量中提取最能体现数据特征差异的2个特征向量成分用于可视化,这就是PCA图UMAPUniform Manifold Approximation and ProjectionUMAP也是一。
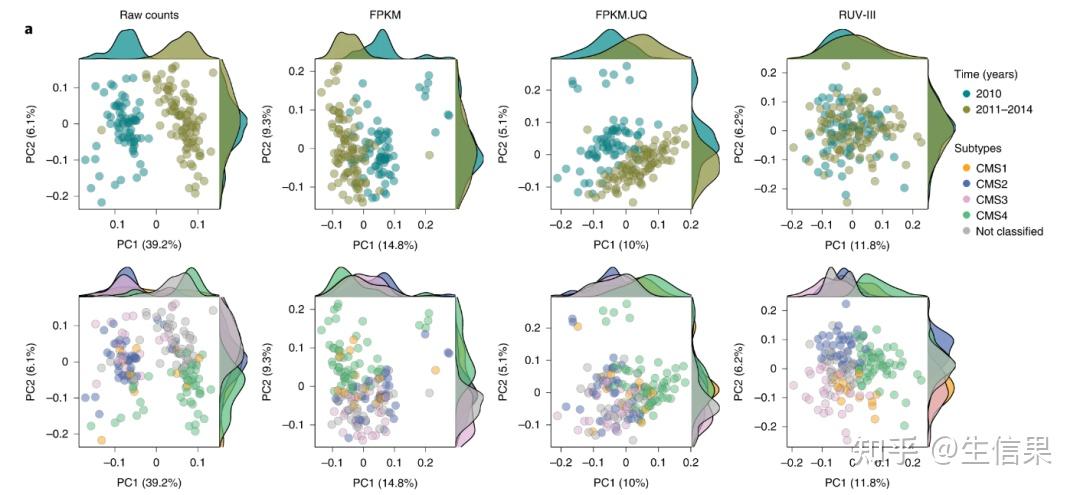
8、PCA分析线性降维的实践 PCA是基于线性模型的降维分析方法,通过寻找能最大程度反映数据规律的坐标系,实现数据降维如图2所示,PCA通过调整光源角度,找到最佳投影平面,直观展示样本间数据分布然而,PCA受限于线性假设,不适用于物种丰度变化范围大或环境梯度变化大的样本PCoA分析基于相似性距离的投影。
9、PCA 核心原理基于线性模型的降维分析方法,通过寻找能最大程度反映数据规律的坐标系,实现数据降维 数据基础直接基于物种丰度数据进行降维 适用场景适用于物种变化较为稳定的环境,但受限于线性假设,不适用于物种丰度变化范围大或环境梯度变化大的样本PCoA 核心原理以样本相似性距离矩阵为。
10、PCA,全称主成分分析,是一种常用于数据降维和特征提取的技术它通过构建一个K维变量空间,将原始数据投影到这个空间中,从而找到数据的主要变化方向,即主成分二PCA的工作原理 数据标准化首先,对数据进行均值居中和单位方差缩放,以确保每个变量在PCA分析中具有相同的重要性构建变量空间构建一。
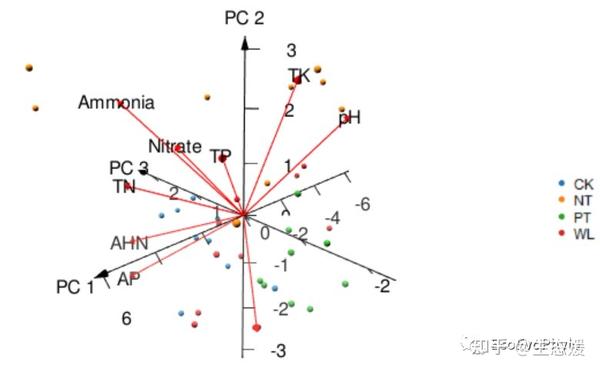
11、PCA分析一文读懂原理 PCA的核心在于通过正交变换减少变量数量,同时保留数据中的大部分信息 它通过消除变量之间的高度相关性,生成互相独立的新主成分,便于后续分析算法 PCA基于协方差矩阵的特征值和特征向量进行计算 关键步骤包括数据的中心化和标准化,以及计算协方差矩阵 通过特征值分解,选择特征值最大的几个特征向。
12、主成分分析PCA介绍及特征降维 一介绍 PCAPrincipal components analysis,即主成分分析,是一种最基本且常用的无监督降维算法PCA可以理解为在空间上对多特征进行坐标系的重划分,确保新的特征之间不存在线性相关,并且损失的信息尽可能少具体来说,PCA利用正交变换即对原坐标系做旋转变换将。
13、PCA主成分分析的简单理解PCA是一种常用的数据降维技术,它可以将高维数据转换到低维空间,同时尽可能保留原始数据的主要信息以下是PCA的简单解释一PCA的核心思想 PCA的核心思想是通过寻找一个变换矩阵,将原始数据从高维空间映射到低维空间,使得在低维空间中,数据的各维度之间相关性最小即。
14、示例展示原始变量对样品的分类 原始数据集包含100个样品的某一基因表达量,通过PCA分析可以观察到样品的分类随着基因数量的增加,分类维度从线性扩展到平面直至三维空间,直观展示了不同基因对分类的贡献筛选变异系数最大的基因进行分类,通过PCA分析,数据呈现出分类模式,进一步优化分类效果PCA实现原理。
15、PCA是一种数据分析方法,它将多个具有相关性的指标重新组合成少量互不相关的综合指标,以达到降维的目的简单通俗的理解 向量与基变换可以想象成我们在一个二维平面上有很多点,如果我们想用一个方向来表示这些点,那么最直观的选择就是这个方向尽可能多地穿过这些点,即这个方向上的方差最大PCA就。