数学集合的符号包括1 大括号表示集合的所有元素2 冒号表示“是的集合”数学集合符号及含义,例如 x x 是自然数表示自然数集合3 空集符号数学集合符号及含义?表示不含任何元素的集合数学集合符号及含义,也称为空集4 子集符号?表示集合A的所有元素都属于集合B,可以包含相同元素5 真子集符号?表示集合A的所有元素数学集合符号及含义;数学集合的符号主要包括以下几个1 N代表非负整数集合,也就是自然数集合,包括0, 1, 2, 3, 等等2 N* 或 N+表示正整数集合,包含1, 2, 3, 等等,但不包括03 Z指整数集合,包括所有整数,如1, 0, 1, 等等,呈无限序列4 Q代表有理数集合,由整数比上整数得到。
符号AB或AB含义在集合A中但不在集合B中的所有元素组成的集合绝对补集符号Arsquo或?u或~A含义在全集U中但不在集合A中的所有元素组成的集合绝对补集是相对于某个给定的全集U而言的这些符号是数学中描述集合及其关系的基本工具,它们帮助我们更准确地表达和理解集合的概念和性质。
绝对补集符号A 或 ?u 或 ~A含义在全集U中但不在集合A中的所有元素组成的集合这通常用于在特定上下文或全集U中讨论集合A的补集总结集合符号用于表示集合之间的关系和运算,是数学中描述集合特性的重要工具理解这些符号的含义,有助于更好地进行集合论的学习和研究。
集合论是数学中的一个重要分支,它研究的是集合这一基本概念以及与之相关的性质和运算在集合论中,有许多符号和术语用来表示集合及其关系以下是一些常见的集合符号及其含义1集合用大写字母表示,如ABC等2元素集合中的每一个对象称为元素,用小写字母表示,如abc等3空集。
集合的符号表示及其含义如下1 全体非负整数的集合通常简称为非负整数集或自然数集,用符号N表示2 非负整数集中排除0的集合,也称正整数集,用符号N+或N*表示3 全体整数的集合通常称作整数集,用符号Z表示4 全体有理数的集合通常简称有理数集,用符号Q表示5 全体实数的。
数学集合符号都有NN+ZQRC等具体介绍如下1全体非负整数的集合通常简称非负整数集或自然数集,记作N2非负整数集内排除0的集,也称正整数集,记作N+或N*3全体整数的集合通常称作整数集,记作Z4全体有理数的集合通常简称有理数集,记作Q5全体实数。
#8834和#8836这四个符号就像导航灯,为我们揭示了集合关系的不同维度首先,让我们深入理解这些基本概念 Subset,它不仅代表着子集或等于的含义,而且当遇到 quotquot 时,它明确了不包含的关系换句话说,当A Subset B时,A是B的一部分,但。
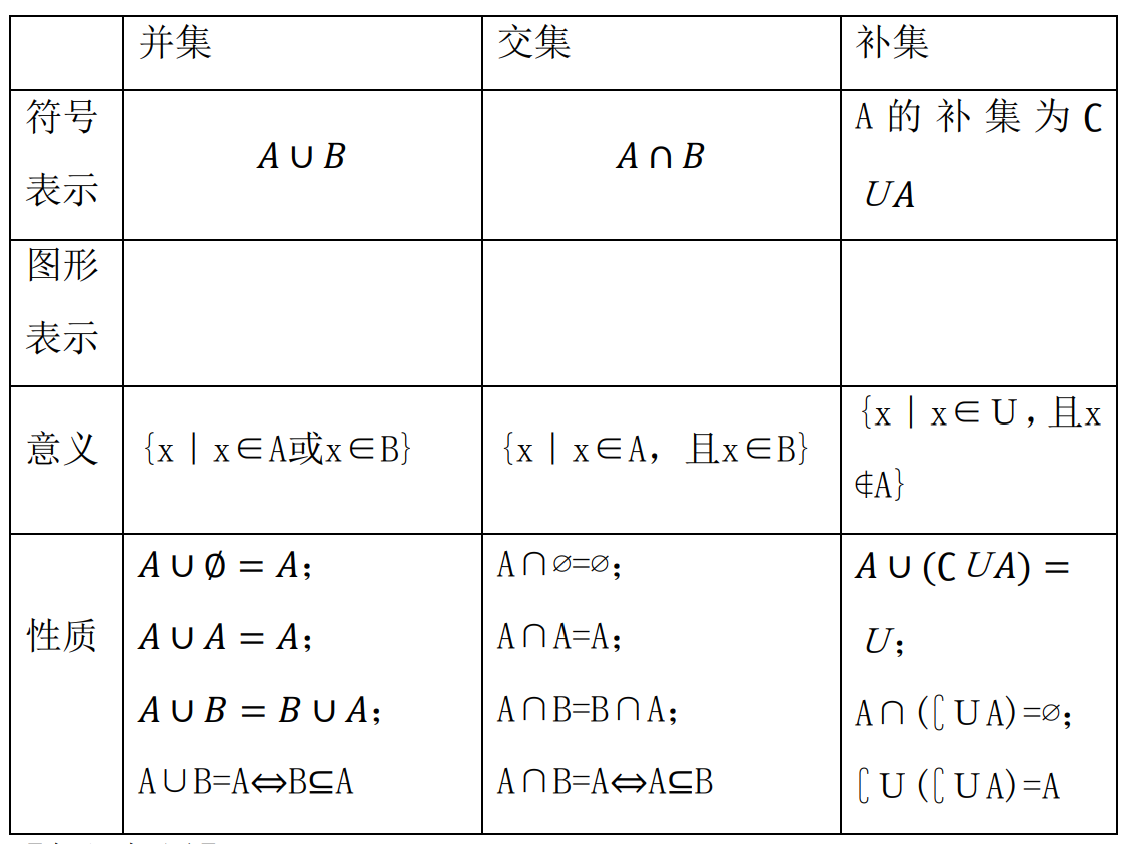
集合的符号表示及意义如下数学集合符号有NN+ZQRC等全体非负整数的集合通常简称非负整数集或自然数集,记作N非负整数集内排除0的集,也称正整数集,记作N+或N*全体整数的集合通常称作整数集,记作Z全体有理数的集合通常简称有理数集,记作Q全体实数的集合通常。
1、数学集合符号及含义如下一数学集合的定义 数学集合是指具有某种特定属性的事物的总体集合论是数学中研究集合的分支,它研究了集合的性质关系运算以及集合之间的映射等在数学中,集合通常用大写字母表示,且成员间没有重复集合的成员可以是有限个数,也可以是无限个数集合可以用描述法表示。
2、1大括号表示集合的符号,例如1,2,3表示由元素123组成的集合2空集符号表示一个不包含任何元素的集合3包含符号表示一个集合包含另一个集合中的所有元素4真包含符号表示一个集合包含另一个集合中的所有元素,并且两个集合不相等5并集符号表示两个集合中所有元素的。
3、数学中,集合的概念是通过一系列特定的符号来表示的以下是一些基本的集合符号及其含义1 N表示自然数集合,包括所有的非负整数2 N+ 或 N*表示正整数集合,即自然数集合中排除零的所有整数3 Z代表整数集合,包括所有的正整数零和负整数4 Q指有理数集合,包含所有可以表示为。
4、不包含于强调了集合间不存在包含关系,即两个集合互不相容,至少在元素层级上没有交集总结,包含于真包含于和不包含于这三个符号在数学中用来描述集合间的包含关系理解这些符号的关键在于认识到它们背后的逻辑和数学含义,即集合间的子集关系严格子集关系以及不存在包含关系通过这些符号,数学家。
5、数学集合的符号及其含义如下非负整数集符号N 含义表示全体非负整数的集合,即包括0和所有正整数正整数集符号N+ 含义表示非负整数集中排除0的集合,即仅包括所有正整数整数集符号Z 含义表示全体整数的集合,包括所有正整数负整数和0有理数集符号Q 含义表示全体有理。