在三门问题中,有三扇门,其中一扇后面有一辆汽车奖品,其余两扇后面是山羊参与者首先选择一扇门,然后主持人会打开另一扇未选择三门问题的门这扇门后面一定是山羊,因为主持人知道汽车在哪扇门后,并询问参与者是否要更换最初三门问题的选择不换的概率如果参与者选择不换门,那么中奖的概率是13这是;三门问题的本质是通过主持人提供的额外信息改变概率分布,其核心在于不同选择下剩余选项的信息量差异导致概率重新分配具体分析如下1 初始概率与信息量基础游戏开始时,三扇门1号2号3号中随机有一扇门后有车,每扇门的初始概率均为13信息量在此指从不确定性到确定性所需的信息量概率。
蒙提霍尔问题,又称三门问题或山羊汽车问题,是一个经典的概率悖论为三门问题了直观理解这个问题,我们可以通过一个具体的例子来进行详细分析问题设定假设有一个游戏节目,节目中有三个外观完全相同的盒子,分别标记为ABC在其中一个盒子里放着一辆汽车代表大奖,另外两个盒子里各放着一只山羊;三门问题与酒鬼问题的区别与联系 一区别 行为人是否有上帝视角 三门问题主持人具有上帝视角,即他明确知道哪扇门后有汽车,哪扇门后有山羊因此,当参赛者选择一扇门后,主持人会故意打开一扇没有汽车但有山羊的门,以影响参赛者的决策这种设计确保了主持人不会打开有汽车的门,从而改变了。
三门问题的解释非计数原理解释三门问题是一个经典的概率悖论,其核心在于通过更换选择来提高获奖的概率这个问题通常描述为有三扇门,其中一扇后面藏有奖品如汽车,另外两扇后面则没有如山羊参与者首先选择一扇门,然后主持人知道奖品所在会打开另一扇没有奖品的门,并询问参与者;三门问题在数学中并不存在真正的争议,而是一个揭示概率论原理的经典谜题以下是关于该问题的详细解答问题描述在三扇门背后分别藏着两只羊和一辆新车,参与者选择一扇门后,主持人会打开其他两扇门中的一扇,然后参与者有机会坚持最初的选择或改变主意直觉与误解大部分人可能会坚持原选,认为有两。
例一常规三门问题中,参赛者先选一扇门,主持人从剩下两扇门中打开一扇有羊的门若仅知道参赛者选了哪扇门,对观众而言相当于三选一,此时每扇门有车的概率看似是13但若以知道主持人打开哪扇门为前提来计算换门或不换门中奖概率,换门中奖概率是23,不换是13这表明主持人打开有羊的门这;蒙提霍尔问题三门问题之最终解答信息泄露 答案在蒙提霍尔问题中,参赛者换门会增加赢得汽车的机会率,即从最初的13提升至23这一结论的关键在于理解信息泄露对概率的影响详细解答问题背景蒙提霍尔问题是一个经典的博弈论问题,源自美国的电视游戏节目参赛者面对三扇关闭的门,其中。
三门问题之所以被视为悖论,主要原因在于它涉及条件概率的理解,并且直观感受与数学计算结果之间存在差异条件概率的影响在三门问题中,参赛者最初选择一扇门时,赢得汽车的概率是13但当主持人打开另一扇没有汽车的门后,剩下的两扇门中哪一扇有汽车的概率就发生了变化这种变化是基于主持人已经。
三门问题的本质是通过信息量的变化分析主观概率的动态调整,核心在于区分“初始选择”与“主持人揭示信息后”的概率空间重构其核心逻辑可拆解为以下要点1 初始选择与概率的静态分布参赛者首次选择时,三扇门1号2号3号中有一扇门后有车,两扇门后有羊此时,猜中车的初始概率均为13,无。
在蒙提霍尔问题中,参赛者应该更换选择以下是详细解释初次选择的概率在初次选择时,每扇门背后隐藏汽车的概率都是13,这是基于随机选择的主持人揭示信息的影响当主持人揭示其中一扇门后的绵羊时,他并非随机选择,而是有意避开汽车所在的门这一行为实际上为参赛者提供了额外的信息更换选择的优势在主持人揭示一扇有羊的门后。
三门问题,也被称为蒙提霍尔问题,是数学和概率论中的一个著名争议这个问题因其直观上的反直觉性而广受讨论问题设定假设你正在参加一个节目,主持人给了你三扇门,门后分别是两只羊和一辆崭新的汽车你需要选择其中一扇门,然后主持人会打开你未选的另外两扇门中藏着羊的那一扇随后,主持人会问你是否要换一扇门直观感受在主持人打开一扇藏着羊。

三门问题之所以被视为悖论,主要原因如下概率的误解在三门问题中,许多人直观上认为,既然一开始选择了一扇门,那么这扇门后面有车的概率就是13,剩下的两扇门各有13的概率因此,当主持人打开一扇没有车的门后,他们错误地认为剩下的两扇门后面有车的概率仍然是相等的然而,实际上,由于。
经典三门问题中,不换选择中奖的概率是13,换选择中奖的概率是23以下是对三门问题及其相关变体的详细解释经典三门问题问题描述共有三道门1,2,3,其中一道门后是一只羊中奖,另外两道门后是空的不中奖参与者随机选择一道门后,主持人会打开剩下两道门中的一道空门,然后。
三门问题的核心误区在于混淆了统计视角下的“概率和”逻辑与单次事件中的“概率或”逻辑,同时错误地将群体统计规律直接套用于个体决策,且未正确理解条件概率的作用 具体分析如下1 统计和逻辑与单次或逻辑的混淆统计视角的“概率和”在大量重复实验中,换门中奖的总次数等于“2号门是车”的次数。
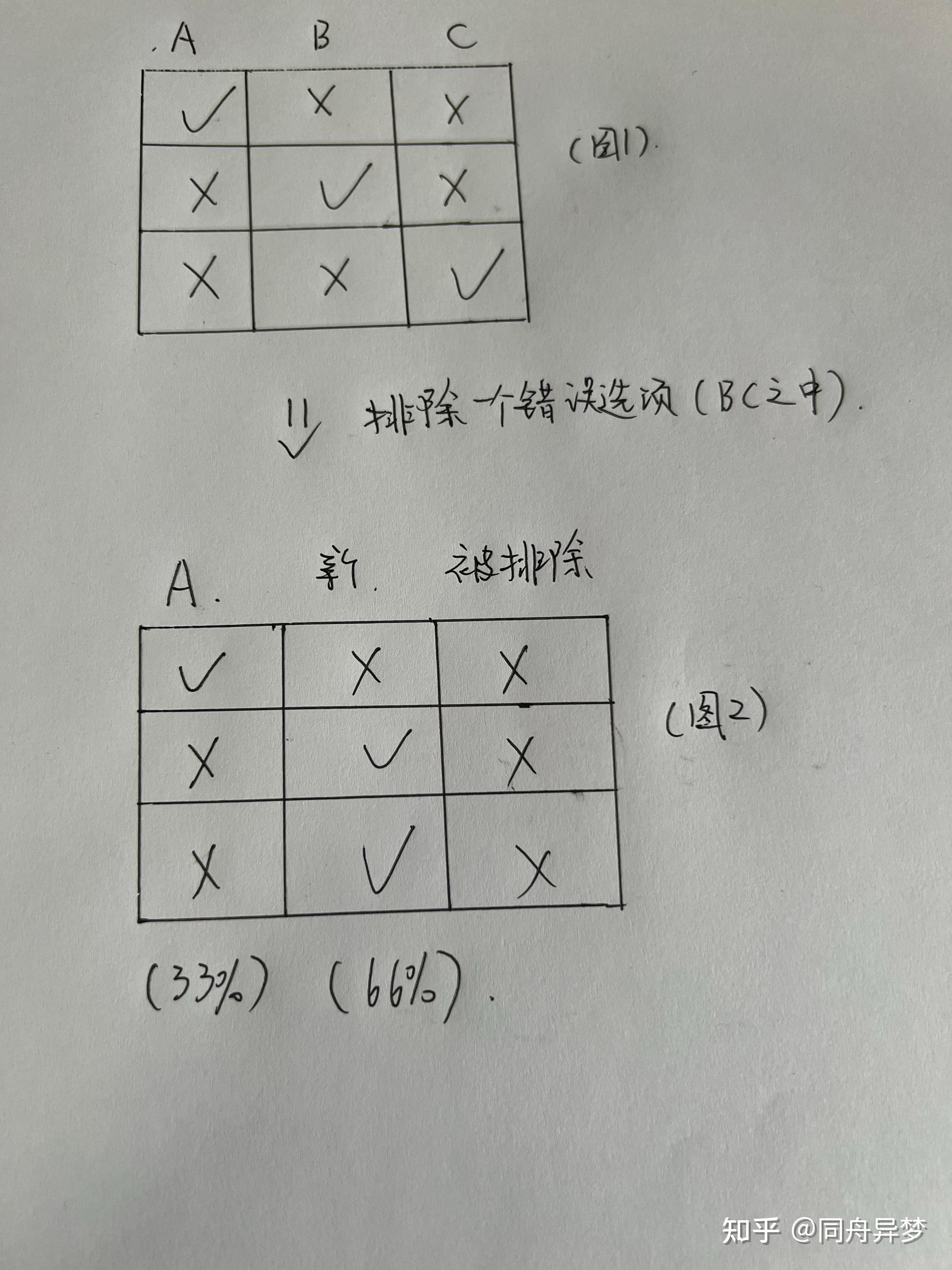
三门问题是一个经典的概率问题,起源于美国电视节目Let#39s Make a Deal该问题通过看似直观的情境,揭示了如何通过概率推理获得最优决策我们将通过贝叶斯理论详细分析这一问题,帮助理解如何应用统计学推理来优化选择问题描述在三门问题中,参赛者面临三扇门背后可能有一辆车奖品,也可能是。
蒙提·霍尔悖论中的三门问题是一个源自博弈论的数学游戏以下是关于三门问题的详细解答问题背景三门问题起源于美国电视游戏节目让我们做一个交易,并以该节目的主持人蒙提·霍尔命名游戏规则玩家面对三扇关闭的门,其中一扇后藏有一辆汽车,玩家选择这扇门即可赢得汽车剩下两扇门后则各有。
三门问题与抓阄问题的解析 三门问题与抓阄问题在本质上都涉及到概率论中的条件概率和样本空间的理解下面,我们将对这两个问题进行详细解析一三门问题 三门问题是一个经典的概率悖论,其内容大致如下假设有三扇门,其中一扇后面有一辆汽车,另外两扇后面各有一只山羊参赛者首先选择其中一扇门。