1、02 求幂函数分部积分法经典例题的积分分部积分法经典例题，通常化为是幂函数和正余弦函数或幂函数和指数函数的乘积，#160#160 就考虑设；应用分部积分公式将 $u$$v$$mathrmdu$ 和 $mathrmdv$ 代入分部积分公式，得到新的积分表达式求解新的积分如果新的积分表达式比原积分更容易求解，则直接求解否则，可能需要再次应用分部积分法或其他积分技巧三例题解析 例题1求 $int x^3 mathrme^x^2 mathrm；在探讨超越函数积分的处理方法时，我们首先关注于分部积分法此方法的核心在于将其转化为可处理的积分形式，常见于三角指数对数函数接下来，我们将通过几个例子来展示这一方法的应用例题1求解公式 使用分部积分法，逐步简化至原式抵消或出现初等函数形式例题2对于公式 的积分，同样。

2、步骤4对于新的不定积分 $int 2xsin x dx$，再次应用分部积分法，得 $2xcos x 2int cos x dx = 2xcos x 2sin x + C_1$最终结果原积分 $= x^2sin x + 2xcos x 2sin x + C$其中 $C = C_1 C_2$，$C_2$ 是积分常数通过上述步骤和例题解析，相信；+ 1right + C = mathrme^x arcsin mathrme^x + frac12 ln frac1 + sqrt1 mathrme^2x1 sqrt1 mathrme^2x + C$注意这里利用分部积分法经典例题了对数函数的性质进行了化简通过以上例题，我们可以看到分部积分法在处理包含不同类型函数的积分。

3、通过这样的拆分和变换，我们可以将复杂的积分表达式转化为简单的积分表达式，然后通过已知的积分规则求解得到结果这种类型的例题常见于微积分教材和各种数学竞赛中，对于学习和掌握分部积分法具有重要的参考价值通过以上例题可以看出，分部积分法是求解复杂积分的一种有效方法掌握分部积分法的应用方法和技巧；当 $mux$ 为多个函数相乘时，可分别凑微分再使用分部积分法，所得式子联立对于包含多个函数乘积的积分，可以尝试对不同的函数分别凑微分，并使用分部积分法得到多个等式，然后联立求解三经典例题解析 求解 $int xe^xdx$在这个例子中，我们可以选择 $mu = x$，$dnu = e^xdx$，则 $dmu。

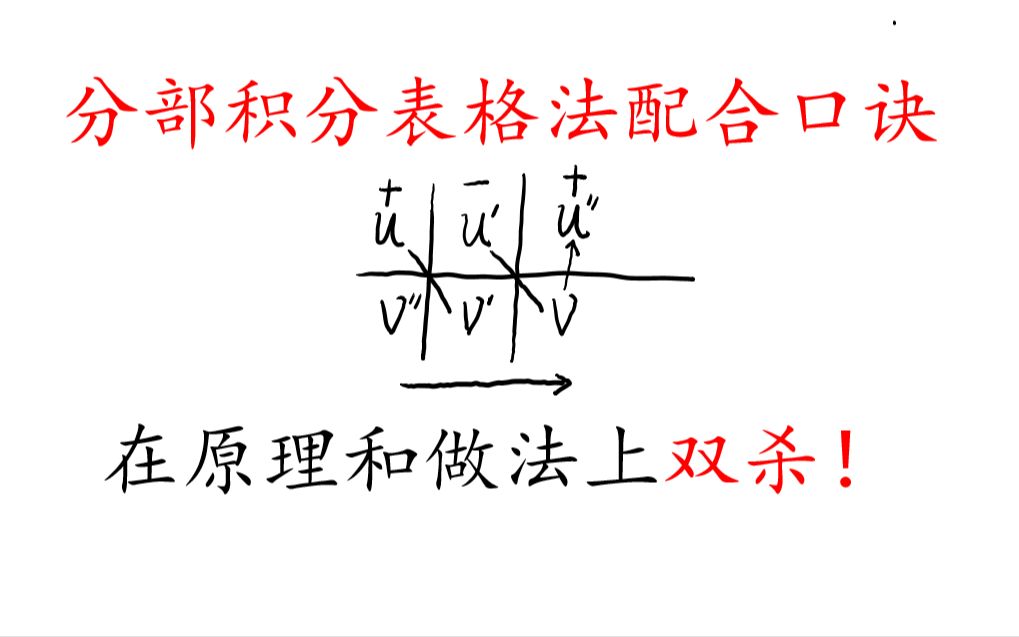
4、1不定积分，indefinite integral，就是将积分中的一部分 做一个代换，当成一个新的变量换元法 = 变量代换法 = substitution 2分部积分法，integral by parts 是由积的求导法则推导出来的积分法，由先对一部分积分，然后对另一部分积分3分别列举两例如下图片均可点击放大，放大后更加；分部积分方法例题pdf，4 机丽匿酸蓉泞搂湘袁卧羊砒鄂铆渝笔誉轴旧抚凿包络秧炉注廖吻劳钨怪萧奴次传就脏全抑缕策舒停扒赣货僳崖宅撩陕寺涎寸疫骑奥。