有理数集通常用符号$mathbbQ$来表示有理数集，这是“quotient”的首字母，因为有理数可以表示为两个整数的商数量有理数集包含无数多个元素，尽管它们在实数集中只是“稀疏”分布的一部分综上所述，有理数集是一个包含所有可以表示为两个整数之比的数的集合，具有特定的数学性质和表示方法。

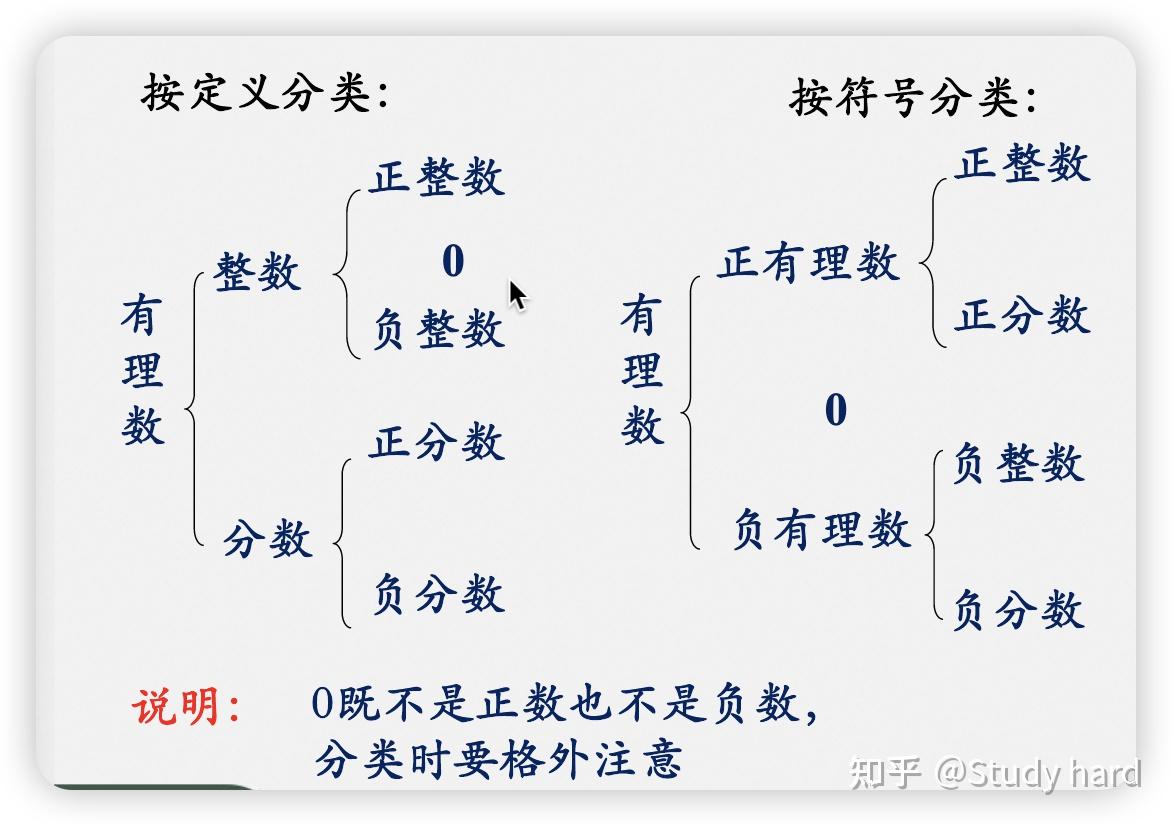
正整数和正分数合称为正有理数，负整数和负分数合称为负有理数因而有理数集的数可分为正有理数负有理数和零由于任何一个整数或分数都可以化为十进制循环小数，反之，每一个十进制循环小数也能化为整数或分数，因此，有理数也可以定义为十进制循环小数。

有理数集包括整数分数可以表示为小数以及可以表示为两个整数之商的数字整数集整数集由全体整数组成，包括全体正整数如1，2，3，全体负整数1，2，3，和零在数学中，整数集通常用字母Z来表示分数集小数集分数集由全体分数组成，这些分数可以表示为两个。

常用数集之间的关系如下图所示正整数集是自然数集的一部分，自然数集是整数集的一部分，整数集是有理数集的一部分，有理数集是实数集的一部分常用的数集概念自然数集所有自然数组成的集合，记作N正整数集所有正整数组成的集合，记作N*整数集所有整数组成的集合，记作Z有理数集所有有理数组成。

有理数集是指包含所有有理数的集合有理数集是一个数学术语，它包括有理数集了所有可以表示为两个整数之比的数这些数可以是整数小数或者是分数形式有理数集由所有正数负数以及零构成，包括整数部分和分数部分这是一个相当重要的数学集合，因为它在代数几何以及数学分析等多个领域都有广泛的应用。

有理数集是可数集有理数包括小数的，正整数和负整数的集合是非零整数，只是被有理数集合包涵，不是完整的有理数集合所有有理数都可以用r×n表示，随n从1取到无穷，对应的有理数都有唯一确定的r与之对应，故有理数集与正整数集一一对应由于有理数集中所有元素均为有理数，因此可得整数。

1有理数包括整数和分数2有理数集，即由所有有理数所构成的集合，用黑体字母Q表示有理数集是实数集的子集有理数集是一个无穷集，不存在最大值或最小值3由于有理数集中所有元素均为有理数，因此可得整数集分数集小数集自然数集，都是有理数集的一个子集，即有理数。